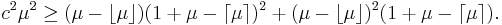Van Houtum distribution
| Probability mass function |
|
| Parameters | ![p_a,p_b \in [0,1] \text{ and } a,b \in \mathbb{Z} \text{ with } a\leq b](/2012-wikipedia_en_all_nopic_01_2012/I/d8f4fc6b38436475e609292cf74aadbc.png) |
|---|---|
| Support | 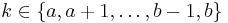 |
| PMF | 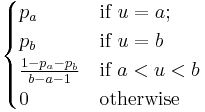 |
| CDF | 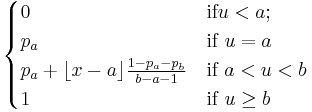 |
| Mean | 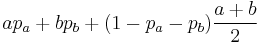 |
| Mode | N/A |
| Variance | 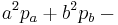
|
| Entropy | 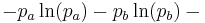
|
| MGF | 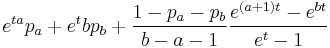 |
| CF | 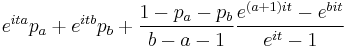 |
In probability theory and statistics, the Van Houtum distribution is a discrete probability distribution named after prof. Geert-Jan van Houtum. It can be characterized by saying that all values of a finite set of possible values are equally probable, except for the smallest and largest element of this set. Since the Van Houtum distribution is a generalization of the discrete uniform distribution, i.e. it is uniform except possibly at its boundaries, it is sometimes also referred to as quasi-uniform.
It is regularly the case that the only available information concerning some discrete random variable variable are its first two moments. The Van Houtum distribution can be used to fit a distribution with finite support on these moments.
A simple example of the Van Houtum distribution arises when throwing a loaded dice which has been tampered with to land on a 6 twice as often as on a 1. The possible values of the sample space are 1, 2, 3, 4, 5 and 6. Each time the die is thrown, the probability of throwing a 2, 3, 4 or 5 is 1/6; the probability of a 1 is 1/18 and the probability of throwing a 6 is 2/9.
Contents |
Probability mass function
A random variable U has a Van Houtum (a, b, pa, pb) distribution if its probability mass function is
Fitting procedure
Suppose a random variable  has mean
has mean  and squared coefficient of variation
and squared coefficient of variation 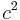 . Let
. Let  be a Van Houtum distributed random variable. Then the first two moments of
be a Van Houtum distributed random variable. Then the first two moments of  match the first two moments of
match the first two moments of  if
if  ,
,  ,
, 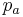 and
and 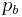 are chosen such that[1]:
are chosen such that[1]:
There does not exist a Van Houtum distribution for every combination of  and
and 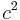 . By using the fact that for any real mean
. By using the fact that for any real mean  the discrete distribution on the integers that has minimal variance is concentrated on the integers
the discrete distribution on the integers that has minimal variance is concentrated on the integers 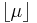 and
and 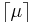 , it is easy to verify that a Van Houtum distribution (or indeed any discrete distribution on the integers) can only be fitted on the first two moments if [2]
, it is easy to verify that a Van Houtum distribution (or indeed any discrete distribution on the integers) can only be fitted on the first two moments if [2]
See also
References
- ^ J.J. Arts (2009), Efficient optimization of the Dual-Index policy using Markov Chain approximations. MSc Thesis, Eindhoven University of Technology, The Netherlands (Appendix B)
- ^ I.J.B.F. Adan, M.J.A. van Eenige, and J.A.C. Resing. "Fitting discrete distributions on the first two moments". Probability in the Engineering and Informational Sciences, 9:623-632, 1996.
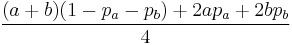
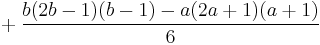
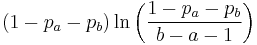
![\Pr(U=u) = \begin{cases} p_a & \text{if } u=a; \\[8pt]
p_b & \text{if } u=b \\[8pt]
\dfrac{1-p_a-p_b}{b-a-1} & \text{if } a<u<b \\[8pt]
0 & \text{otherwise} \end{cases}](/2012-wikipedia_en_all_nopic_01_2012/I/cacdb7d1b8081fa8b8d22837146a0f70.png)
![\begin{align}
a &= \left\lceil \mu - \frac{1}{2} \left\lceil \sqrt{1%2B12c^2\mu^2} \right\rceil \right\rceil \\[8pt]
b &= \left\lfloor \mu %2B \frac{1}{2} \left\lceil \sqrt{1%2B12c^2\mu^2} \right\rceil \right\rfloor \\[8pt]
p_b &= \frac{(c^2%2B1)\mu^2-A-(a^2-A)(2\mu-a-b)/(a-b)}{a^2%2Bb^2-2A} \\[8pt]
p_a &= \frac{2\mu-a-b}{a-b}%2Bp_b \\[12pt]
\text{where } A & = \frac{2a^2%2Ba%2B2ab-b%2B2b^2}{6}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/0dd4af8c98ebdb00e73f6169e041a712.png)